Density Module#

Overview

`freud.density.CorrelationFunction`	Computes the complex pairwise correlation function.
`freud.density.GaussianDensity`	Computes the density of a system on a grid.
`freud.density.LocalDensity`	Computes the local density around a particle.
`freud.density.RDF`	Computes the RDF \(g \left( r \right)\) for supplied data.
`freud.density.SphereVoxelization`	Computes a grid of voxels occupied by spheres.

Details

The freud.density module contains various classes relating to the density of the system. These functions allow evaluation of particle distributions with respect to other particles.

class freud.density.CorrelationFunction#

Bases: _SpatialHistogram1D

Computes the complex pairwise correlation function.

The correlation function is given by \(C(r) = \left\langle s^*_1(0) \cdot s_2(r) \right\rangle\) between two sets of points \(p_1\) (points) and \(p_2\) (query_points) with associated values \(s_1\) (values) and \(s_2\) (query_values). Computing the correlation function results in an array of the expected (average) product of all values at a given radial distance \(r\). The values of \(r\) where the correlation function is computed are controlled by the bins and r_max parameters to the constructor, and the spacing between the bins is given by dr = r_max / bins.

Note

Self-correlation: It is often the case that we wish to compute the correlation function of a set of points with itself. If query_points is the same as points, not provided, or None, we omit accumulating the self-correlation value in the first bin.

Parameters:

bins (unsigned int) – The number of bins in the correlation function.
r_max (float) – Maximum pointwise distance to include in the calculation.

bin_centers#

The centers of each bin in the histogram.

Type:: \((N_{bins}, )\) numpy.ndarray

property bin_counts#

The bin counts in the histogram.

Type:: numpy.ndarray

bin_edges#

The edges of each bin in the histogram. It is one element larger because each bin has a lower and an upper bound.

Type:: \((N_{bins}+1, )\) numpy.ndarray

bounds#

A tuple indicating upper and lower bounds of the histogram.

Type:: tuple

property box#

The box object used in the last computation.

Type:: freud.box.Box

compute(self, system, values, query_points=None, query_values=None, neighbors=None, reset=True)#

Calculates the correlation function and adds to the current histogram.

Parameters:

system – Any object that is a valid argument to freud.locality.NeighborQuery.from_system.
values ((\(N_{points}\)) numpy.ndarray) – Values associated with the system points used to calculate the correlation function.
query_points ((\(N_{query\_points}\), 3) numpy.ndarray, optional) – Query points used to calculate the correlation function. Uses the system’s points if None (Default value = None).
query_values ((\(N_{query\_points}\)) numpy.ndarray, optional) – Query values used to calculate the correlation function. Uses values if None. (Default value = None).
neighbors (freud.locality.NeighborList or dict, optional) – Either a NeighborList of neighbor pairs to use in the calculation, or a dictionary of query arguments (Default value: None).
reset (bool) – Whether to erase the previously computed values before adding the new computation; if False, will accumulate data (Default value: True).

property correlation#

Expected (average) product of all values at a given radial distance.

Type:: (\(N_{bins}\)) numpy.ndarray

default_query_args#: The default query arguments are {'mode': 'ball', 'r_max': self.r_max}.

nbins#

The number of bins in the histogram.

Type:: int

plot(self, ax=None)#

Plot complex correlation function.

Parameters:: ax (matplotlib.axes.Axes, optional) – Axis to plot on. If None, make a new figure and axis. (Default value = None)
Returns:: Axis with the plot.
Return type:: (matplotlib.axes.Axes)

class freud.density.GaussianDensity#

Bases: _Compute

Computes the density of a system on a grid.

Replaces particle positions with a Gaussian blur and calculates the contribution from each to the proscribed grid based upon the distance of the grid cell from the center of the Gaussian. The weights for the Gaussians could be additionally specified in the compute method. The convolution of the weights with the Gaussians is calculated in this case:

\[p(\vec{r}) = \sum_i \frac{1}{2\pi \sigma^2} \exp \left(-\frac{(\vec{r}-\vec{r}_i)^2}{2\sigma^2}\right) p_i\]

The resulting data is a regular grid of particle densities or convolved parameter that can be used in standard algorithms requiring evenly spaced point, such as Fast Fourier Transforms. The dimensions of the grid are set in the constructor, and can either be set equally for all dimensions or for each dimension independently.

Parameters:

width (int or Sequence[int]) – The number of bins to make the grid in each dimension (identical in all dimensions if a single integer value is provided).
r_max (float) – Distance over which to blur.
sigma (float) – Sigma parameter for Gaussian.

property box#

Box used in the calculation.

Type:: freud.box.Box

compute(self, system, values=None)#

Calculates the Gaussian blur for the specified points.

Parameters:

system – Any object that is a valid argument to freud.locality.NeighborQuery.from_system.
values ((\(N_{points}\)) numpy.ndarray) – Values associated with the system points used to calculate the convolution. Calculates Gaussian blur (equivalent to providing a value of 1 for every point) if None. (Default value = None).

property density#

The grid with the Gaussian density contributions from each point.

Type:: (\(w_x\), \(w_y\), \(w_z\)) numpy.ndarray

plot(self, ax=None)#

Plot Gaussian Density.

Parameters:: ax (matplotlib.axes.Axes, optional) – Axis to plot on. If None, make a new figure and axis. (Default value = None)
Returns:: Axis with the plot.
Return type:: (matplotlib.axes.Axes)

r_max#

Distance over which to blur.

Type:: float

sigma#

Sigma parameter for Gaussian.

Type:: float

width#

The number of bins in the grid in each dimension (identical in all dimensions if a single integer value is provided).

Type:: tuple[int]

class freud.density.LocalDensity#

Bases: _PairCompute

Computes the local density around a particle.

The density of the local environment is computed and averaged for a given set of query points in a sea of data points. Providing the same points calculates them against themselves. Computing the local density results in an array listing the value of the local density around each query point. Also available is the number of neighbors for each query point, giving the user the ability to count the number of particles in that region. Note that the computed density is essentially a number density (allowing for fractional values as described below). If particles have a specific volume, a volume density can be computed by simply multiplying the number density by the volume of the particles.

In order to provide sufficiently smooth data, data points can be fractionally counted towards the density. Rather than perform compute-intensive area (volume) overlap calculations to determine the exact amount of overlap area (volume), the LocalDensity class performs a simple linear interpolation relative to the centers of the data points. Specifically, a point is counted as one neighbor of a given query point if it is entirely contained within the r_max, half of a neighbor if the distance to its center is exactly r_max, and zero if its center is a distance greater than or equal to r_max + diameter from the query point’s center. Graphically, this looks like: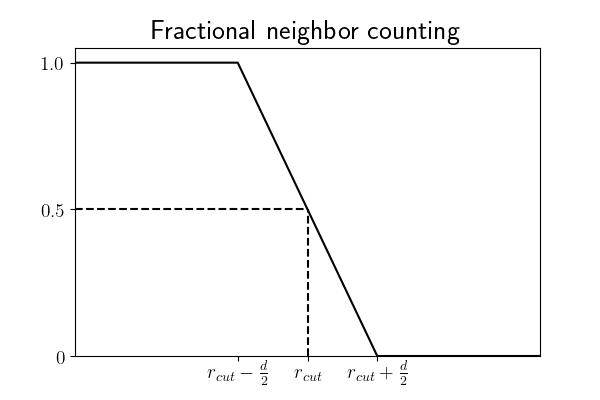

Parameters:

r_max (float) – Maximum distance over which to calculate the density.
diameter (float) – Diameter of particle circumsphere.

property box#

Box used in the calculation.

Type:: freud.box.Box

compute(self, system, query_points=None, neighbors=None)#

Calculates the local density for the specified points.

Example:

>>> import freud
>>> box, points = freud.data.make_random_system(10, 100, seed=0)
>>> # Compute Local Density
>>> ld = freud.density.LocalDensity(r_max=3, diameter=0.05)
>>> ld.compute(system=(box, points))
freud.density.LocalDensity(...)

Parameters:

system – Any object that is a valid argument to freud.locality.NeighborQuery.from_system.
query_points ((\(N_{query\_points}\), 3) numpy.ndarray, optional) – Query points used to calculate the correlation function. Uses the system’s points if None (Default value = None).
neighbors (freud.locality.NeighborList or dict, optional) –
Either a NeighborList of neighbor pairs to use in the calculation, or a dictionary of query arguments (Default value: None).

default_query_args#: The default query arguments are {'mode': 'ball', 'r_max': self.r_max + 0.5*self.diameter}.

property density#

Density of points per query point.

Type:: (\(N_{points}\)) numpy.ndarray

diameter#

Diameter of particle circumsphere.

Type:: float

property num_neighbors#

Number of neighbor points for each query point.

Type:: (\(N_{points}\)) numpy.ndarray

r_max#

Maximum distance over which to calculate the density.

Type:: float

class freud.density.RDF#

Bases: _SpatialHistogram1D

Computes the RDF \(g \left( r \right)\) for supplied data.

Note that the RDF is defined strictly according to the pair correlation function, i.e.

\[g(r) = V\frac{N-1}{N} \langle \delta(r) \rangle\]

In the thermodynamic limit, the fraction tends to unity and the limiting behavior of \(\lim_{r \to \infty} g(r)=1\) is recovered. However, for very small systems the long range behavior of the radial distribution will instead tend to \(\frac{N-1}{N}\). In small systems, where this deviation is noticeable, the normalization_mode argument may be used to rescale the results and force the long range behavior to 1. Note that this option will have little to no effect on larger systems (for example, for systems of 100 particles the RDF will differ by 1%).

Note

For correct normalization behavior, let the set of points be either: 1) the same as the set of query points or 2) completely disjoint from the set of query points (points shouldn’t contain any particles in query points).

Note

For correct normalization behavior when using normalization_mode='finite_size', the points _must_ be the same as the query_points and exclude_ii must be set to False.

Note

2D: freud.density.RDF properly handles 2D boxes. The points must be passed in as [x, y, 0].

Parameters:

bins (unsigned int) – The number of bins in the RDF.
r_max (float) – Maximum interparticle distance to include in the calculation.
r_min (float, optional) – Minimum interparticle distance to include in the calculation (Default value = 0).
normalization_mode (str, optional) – There are two valid string inputs for this argument. The first option, exact, handles the normalization as shown mathematically at the beginning of this class’s docstring. The other option, finite_size, adds an extra rescaling factor of \(\frac{N_{query\_points}}{N_{query\_ponts} - 1}\) so the RDF values will tend to 1 at large \(r\) for small systems (Default value = 'exact').

bin_centers#

The centers of each bin in the histogram.

Type:: \((N_{bins}, )\) numpy.ndarray

property bin_counts#

The bin counts in the histogram.

Type:: numpy.ndarray

bin_edges#

The edges of each bin in the histogram. It is one element larger because each bin has a lower and an upper bound.

Type:: \((N_{bins}+1, )\) numpy.ndarray

bounds#

A tuple indicating upper and lower bounds of the histogram.

Type:: tuple

property box#

The box object used in the last computation.

Type:: freud.box.Box

compute(self, system, query_points=None, neighbors=None, reset=True)#

Calculates the RDF and adds to the current RDF histogram.

Parameters:

system – Any object that is a valid argument to freud.locality.NeighborQuery.from_system.
query_points ((\(N_{query\_points}\), 3) numpy.ndarray, optional) – Query points used to calculate the RDF. Uses the system’s points if None (Default value = None).
neighbors (freud.locality.NeighborList or dict, optional) –
Either a NeighborList of neighbor pairs to use in the calculation, or a dictionary of query arguments (Default value: None).
reset (bool) – Whether to erase the previously computed values before adding the new computation; if False, will accumulate data (Default value: True).

default_query_args#: The default query arguments are {'mode': 'ball', 'r_max': self.r_max}.

property n_r#

Histogram of cumulative bin_counts values. More precisely, n_r[i] is the average number of points contained within a ball of radius bin_edges[i+1] centered at a given query_point averaged over all query_points in the last call to compute().

Type:: (\(N_{bins}\),) numpy.ndarray

nbins#

The number of bins in the histogram.

Type:: int

plot(self, ax=None)#

Plot radial distribution function.

Parameters:: ax (matplotlib.axes.Axes, optional) – Axis to plot on. If None, make a new figure and axis. (Default value = None)
Returns:: Axis with the plot.
Return type:: (matplotlib.axes.Axes)

property rdf#

Histogram of RDF values.

Type:: (\(N_{bins}\),) numpy.ndarray

class freud.density.SphereVoxelization#

Bases: _Compute

Computes a grid of voxels occupied by spheres.

This class constructs a grid of voxels. From a given set of points and a desired radius, a set of spheres are created. The voxels are assigned a value of 1 if their center is contained in one or more spheres and 0 otherwise. The dimensions of the grid are set in the constructor, and can either be set equally for all dimensions or for each dimension independently.

Parameters:

width (int or Sequence[int]) – The number of bins to make the grid in each dimension (identical in all dimensions if a single integer value is provided).
r_max (float) – Sphere radius.

property box#

Box used in the calculation.

Type:: freud.box.Box

compute(self, system)#

Calculates the voxelization of spheres about the specified points.

Parameters:: system – Any object that is a valid argument to freud.locality.NeighborQuery.from_system.

plot(self, ax=None)#

Plot voxelization.

Parameters:: ax (matplotlib.axes.Axes, optional) – Axis to plot on. If None, make a new figure and axis. (Default value = None)
Returns:: Axis with the plot.
Return type:: (matplotlib.axes.Axes)

r_max#

Sphere radius used for voxelization.

Type:: float

property voxels#

The voxel grid indicating overlap with the computed spheres.

Type:: (\(w_x\), \(w_y\), \(w_z\)) numpy.ndarray

width#

The number of bins in the grid in each dimension (identical in all dimensions if a single integer value is provided).

Type:: tuple[int]