freud.order.Hexatic: 2D Minkowski Structure Metrics¶
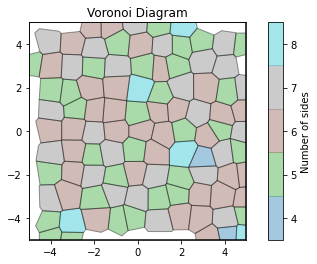
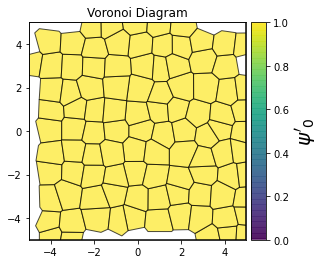
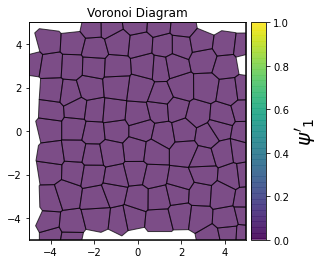
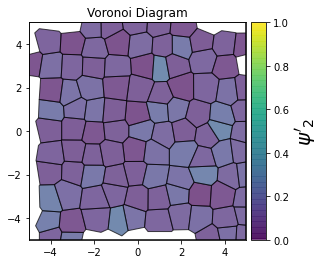
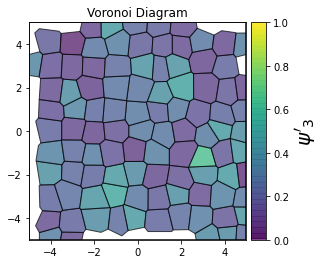
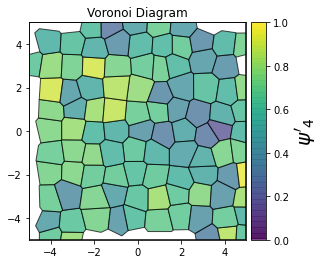
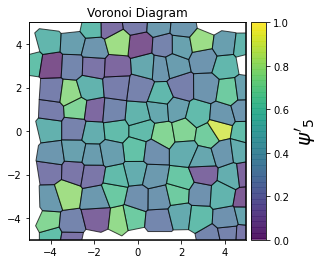
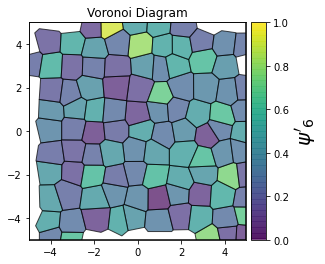
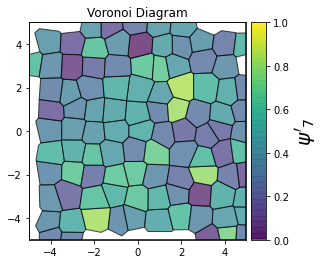
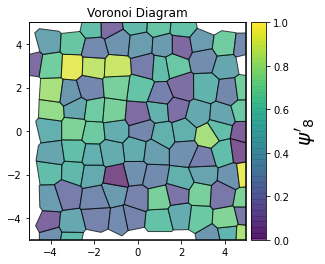
This demonstrates a variant of the hexatic order parameter \(\psi_k\) that weighs each neighbor bond according to its corresponding side length in a Voronoi diagram of the system. This variant, called a Minkowski Structure Metric, is invariant under rotation, translation, and scaling. We denote the 2D Minkowski Structure Metric (the Voronoi-weighted form of the hexatic order parameter) as \(\psi'_k\).
See also: - https://morphometry.org/theory/anisotropy-analysis-by-imt/ - https://aip.scitation.org/doi/10.1063/1.4774084
[1]:
import freud
import numpy as np
from matplotlib.colorbar import Colorbar
from mpl_toolkits.axes_grid1.axes_divider import make_axes_locatable
[2]:
def show_minkowski_structure_metrics(system):
voro = freud.locality.Voronoi()
voro.compute(system)
voro.plot()
for k in [0, 1, 2, 3, 4, 5, 6, 7, 8]:
psi = freud.order.Hexatic(k=k, weighted=True)
psi.compute(system, neighbors=voro.nlist)
order = np.absolute(psi.particle_order)
ax = voro.plot()
patches = ax.collections[0]
patches.set_array(order)
patches.set_cmap("viridis")
patches.set_clim(0, 1)
patches.set_alpha(0.7)
# Remove old colorbar coloring by number of sides
ax.figure.delaxes(ax.figure.axes[-1])
ax_divider = make_axes_locatable(ax)
# Add a new colorbar to the right of the main axes.
cax = ax_divider.append_axes("right", size="7%", pad="2%")
cbar = Colorbar(cax, patches)
cbar.set_label(rf"$\psi'_{k}$", size=20)
ax
[3]:
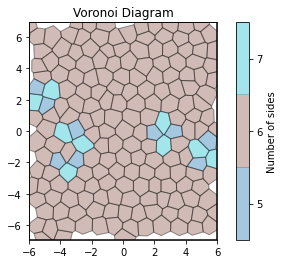
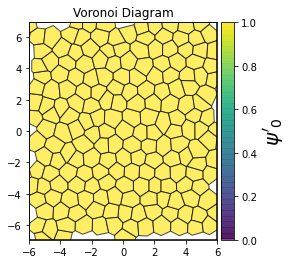
unit_cell = freud.data.UnitCell.hex()
system = unit_cell.generate_system(num_replicas=[12, 8, 1], sigma_noise=0.15)
show_minkowski_structure_metrics(system)
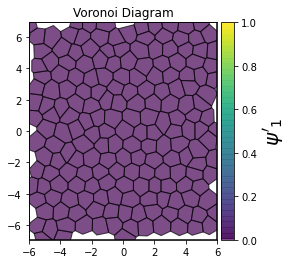
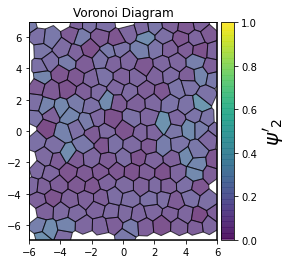
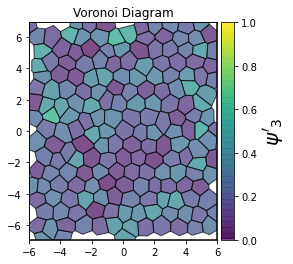
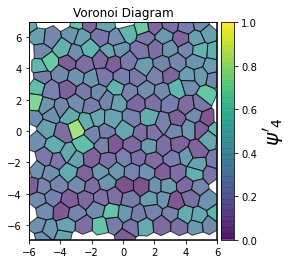
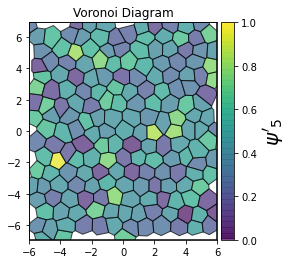

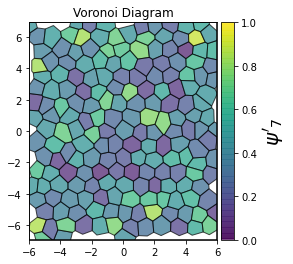
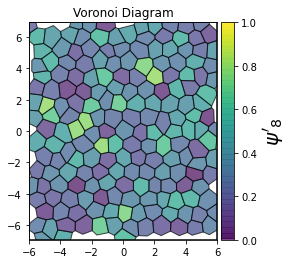
[4]:
unit_cell = freud.data.UnitCell.square()
system = unit_cell.generate_system(num_replicas=10, sigma_noise=0.15)
show_minkowski_structure_metrics(system)