Analyzing data from LAMMPS¶
The following script shows how to use freud to compute the radial distribution function \(g(r)\) on data generated by the molecular dynamics simulation engine LAMMPS. The input script runs a Lennard-Jones system, which is then parsed with numpy.genfromtxt.
The input script is below. Note that we must dump images with ix iy iz, so that the mean squared displacement can be calculated correctly.
[1]:
!cat lj.in
Next, we run LAMMPS to generate the output file. LAMMPS can be installed with conda install -c conda-forge lammps.
[2]:
!lmp_serial -in lj.in
LAMMPS (5 Jun 2019)
Created orthogonal box = (0 0 0) to (10 10 10)
1 by 1 by 1 MPI processor grid
Lattice spacing in x,y,z = 1.25992 1.25992 1.25992
Created 512 atoms
create_atoms CPU = 0.00142598 secs
Neighbor list info ...
update every 1 steps, delay 10 steps, check yes
max neighbors/atom: 2000, page size: 100000
master list distance cutoff = 2.8
ghost atom cutoff = 2.8
binsize = 1.4, bins = 8 8 8
1 neighbor lists, perpetual/occasional/extra = 1 0 0
(1) pair lj/cut, perpetual
attributes: half, newton on
pair build: half/bin/newton
stencil: half/bin/3d/newton
bin: standard
Setting up Verlet run ...
Unit style : lj
Current step : 0
Time step : 0.005
Per MPI rank memory allocation (min/avg/max) = 6.109 | 6.109 | 6.109 Mbytes
Step PotEng KinEng TotEng Temp Press Density
0 -1804.3284 766.5 -1037.8284 1 -2.1872025 0.512
100 -1834.8127 774.55302 -1060.2596 1.0105062 -0.32671112 0.512
200 -1852.2773 789.53605 -1062.7413 1.0300536 -0.30953463 0.512
300 -1857.4621 795.78772 -1061.6744 1.0382097 -0.22960441 0.512
400 -1864.766 801.81089 -1062.9551 1.0460677 -0.24901206 0.512
500 -1860.0198 796.65657 -1063.3633 1.0393432 -0.14280039 0.512
600 -1859.1835 796.96259 -1062.221 1.0397425 -0.2828161 0.512
700 -1848.9874 786.01864 -1062.9688 1.0254646 -0.34512435 0.512
800 -1821.7263 759.86418 -1061.8622 0.9913427 -0.1766353 0.512
900 -1840.7256 777.68022 -1063.0453 1.0145861 -0.318844 0.512
1000 -1862.6606 799.32963 -1063.3309 1.0428306 -0.25224674 0.512
Loop time of 0.201545 on 1 procs for 1000 steps with 512 atoms
Performance: 2143441.910 tau/day, 4961.671 timesteps/s
99.2% CPU use with 1 MPI tasks x no OpenMP threads
MPI task timing breakdown:
Section | min time | avg time | max time |%varavg| %total
---------------------------------------------------------------
Pair | 0.13586 | 0.13586 | 0.13586 | 0.0 | 67.41
Bond | 8.75e-05 | 8.75e-05 | 8.75e-05 | 0.0 | 0.04
Neigh | 0.05059 | 0.05059 | 0.05059 | 0.0 | 25.10
Comm | 0.0088689 | 0.0088689 | 0.0088689 | 0.0 | 4.40
Output | 0.0002439 | 0.0002439 | 0.0002439 | 0.0 | 0.12
Modify | 0.0044417 | 0.0044417 | 0.0044417 | 0.0 | 2.20
Other | | 0.001454 | | | 0.72
Nlocal: 512 ave 512 max 512 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Nghost: 1447 ave 1447 max 1447 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Neighs: 12018 ave 12018 max 12018 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Total # of neighbors = 12018
Ave neighs/atom = 23.4727
Ave special neighs/atom = 0
Neighbor list builds = 100
Dangerous builds = 100
Setting up Verlet run ...
Unit style : lj
Current step : 1000
Time step : 0.005
Per MPI rank memory allocation (min/avg/max) = 6.109 | 6.109 | 6.109 Mbytes
Step PotEng KinEng TotEng Temp Press Density
1000 -1862.6606 799.32963 -1063.3309 1.0428306 -0.25224674 0.512
1100 -1853.4242 819.28434 -1034.1399 1.0688641 -0.16446166 0.512
1200 -1840.5875 793.33971 -1047.2477 1.0350159 -0.21578932 0.512
1300 -1838.9016 796.0771 -1042.8245 1.0385872 -0.19354995 0.512
1400 -1848.5392 752.5312 -1096.008 0.98177587 -0.22928676 0.512
1500 -1856.8763 746.44097 -1110.4353 0.97383035 -0.18936813 0.512
1600 -1869.5931 732.08398 -1137.5091 0.95509978 -0.2751998 0.512
1700 -1887.7451 761.66169 -1126.0834 0.99368779 -0.35301947 0.512
1800 -1882.9325 729.51153 -1153.421 0.95174368 -0.33872437 0.512
1900 -1867.9452 763.40829 -1104.5369 0.99596646 -0.30614623 0.512
2000 -1874.4475 752.8181 -1121.6294 0.98215017 -0.30908533 0.512
Loop time of 0.206815 on 1 procs for 1000 steps with 512 atoms
Performance: 2088823.301 tau/day, 4835.239 timesteps/s
98.9% CPU use with 1 MPI tasks x no OpenMP threads
MPI task timing breakdown:
Section | min time | avg time | max time |%varavg| %total
---------------------------------------------------------------
Pair | 0.13859 | 0.13859 | 0.13859 | 0.0 | 67.01
Bond | 9.3222e-05 | 9.3222e-05 | 9.3222e-05 | 0.0 | 0.05
Neigh | 0.05101 | 0.05101 | 0.05101 | 0.0 | 24.66
Comm | 0.0086555 | 0.0086555 | 0.0086555 | 0.0 | 4.19
Output | 0.00020504 | 0.00020504 | 0.00020504 | 0.0 | 0.10
Modify | 0.0067122 | 0.0067122 | 0.0067122 | 0.0 | 3.25
Other | | 0.001549 | | | 0.75
Nlocal: 512 ave 512 max 512 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Nghost: 1464 ave 1464 max 1464 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Neighs: 11895 ave 11895 max 11895 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Total # of neighbors = 11895
Ave neighs/atom = 23.2324
Ave special neighs/atom = 0
Neighbor list builds = 100
Dangerous builds = 100
Setting up Verlet run ...
Unit style : lj
Current step : 2000
Time step : 0.005
Per MPI rank memory allocation (min/avg/max) = 7.383 | 7.383 | 7.383 Mbytes
Step PotEng KinEng TotEng Temp Press Density
2000 -1874.4475 752.8181 -1121.6294 0.98215017 -0.30908533 0.512
2100 -1858.3201 763.1433 -1095.1768 0.99562074 -0.25351893 0.512
2200 -1866.9213 770.43352 -1096.4878 1.0051318 -0.27646217 0.512
2300 -1879.7957 721.28174 -1158.514 0.94100683 -0.31881659 0.512
2400 -1886.0524 740.29981 -1145.7526 0.96581841 -0.36988824 0.512
2500 -1862.4955 731.77932 -1130.7162 0.95470231 -0.23656666 0.512
2600 -1847.542 748.14185 -1099.4002 0.97604938 -0.22297358 0.512
2700 -1863.1603 715.01181 -1148.1485 0.93282689 -0.27535839 0.512
2800 -1858.9263 711.64082 -1147.2855 0.92842899 -0.31272288 0.512
2900 -1862.0527 788.4678 -1073.5849 1.0286599 -0.20135611 0.512
3000 -1848.1516 797.66227 -1050.4894 1.0406553 -0.27353978 0.512
3100 -1883.8621 793.05475 -1090.8073 1.0346442 -0.29972206 0.512
3200 -1890.4065 791.32467 -1099.0819 1.032387 -0.35642545 0.512
3300 -1859.2997 745.34089 -1113.9588 0.97239516 -0.26722308 0.512
3400 -1869.8929 762.57135 -1107.3216 0.99487457 -0.14226646 0.512
3500 -1879.6557 732.72846 -1146.9273 0.95594058 -0.21775981 0.512
3600 -1899.0227 766.18046 -1132.8422 0.99958312 -0.2798366 0.512
3700 -1872.6895 817.06218 -1055.6273 1.065965 -0.23193326 0.512
3800 -1891.1356 802.56843 -1088.5672 1.047056 -0.23387156 0.512
3900 -1840.088 753.28729 -1086.8007 0.98276228 -0.21465531 0.512
4000 -1882.7617 803.22857 -1079.5332 1.0479172 -0.31896543 0.512
4100 -1873.9061 787.05281 -1086.8533 1.0268138 -0.26608644 0.512
4200 -1871.6627 832.59728 -1039.0655 1.0862326 -0.29040189 0.512
4300 -1865.3725 819.61212 -1045.7603 1.0692917 -0.22592305 0.512
4400 -1875.5306 806.71297 -1068.8176 1.0524631 -0.31604788 0.512
4500 -1857.109 828.16158 -1028.9474 1.0804456 -0.2464398 0.512
4600 -1857.8912 729.7257 -1128.1655 0.9520231 -0.31385004 0.512
4700 -1842.205 734.17836 -1108.0267 0.95783217 -0.27130372 0.512
4800 -1864.7696 776.14641 -1088.6232 1.012585 -0.31668109 0.512
4900 -1858.1103 793.41913 -1064.6911 1.0351195 -0.16583366 0.512
5000 -1867.7818 815.23276 -1052.5491 1.0635783 -0.28680645 0.512
5100 -1838.0477 725.412 -1112.6357 0.9463953 -0.28647867 0.512
5200 -1810.7731 731.9772 -1078.7959 0.95496047 -0.16033508 0.512
5300 -1837.5311 749.48424 -1088.0469 0.97780071 -0.20281441 0.512
5400 -1873.1094 764.60064 -1108.5088 0.99752204 -0.41358648 0.512
5500 -1888.9361 748.61774 -1140.3184 0.97667025 -0.36938658 0.512
5600 -1869.9513 762.05258 -1107.8988 0.99419776 -0.4223791 0.512
5700 -1858.339 746.55871 -1111.7803 0.97398396 -0.42269281 0.512
5800 -1863.2613 749.34951 -1113.9118 0.97762493 -0.38710722 0.512
5900 -1873.7293 773.93107 -1099.7982 1.0096948 -0.26021895 0.512
6000 -1873.456 787.00426 -1086.4518 1.0267505 -0.22677264 0.512
6100 -1856.3965 789.71834 -1066.6782 1.0302914 -0.23662444 0.512
6200 -1868.1487 781.09973 -1087.0489 1.0190473 -0.13471937 0.512
6300 -1873.9941 740.70637 -1133.2877 0.96634882 -0.26089329 0.512
6400 -1879.5293 758.83006 -1120.6993 0.98999355 -0.40717493 0.512
6500 -1873.208 730.21233 -1142.9956 0.95265797 -0.33679524 0.512
6600 -1893.088 738.17171 -1154.9163 0.96304202 -0.34898503 0.512
6700 -1854.9994 735.97428 -1119.0252 0.96017518 -0.28228204 0.512
6800 -1841.9759 797.06384 -1044.9121 1.0398745 -0.19145452 0.512
6900 -1850.4935 786.14747 -1064.3461 1.0256327 -0.29327665 0.512
7000 -1845.6749 797.15417 -1048.5207 1.0399924 -0.45867335 0.512
7100 -1831.03 827.34343 -1003.6866 1.0793782 -0.179498 0.512
7200 -1888.1042 749.22706 -1138.8771 0.97746518 -0.53010406 0.512
7300 -1859.9233 754.0352 -1105.8881 0.98373803 -0.39545192 0.512
7400 -1851.9183 787.60897 -1064.3093 1.0275394 -0.37094061 0.512
7500 -1848.0739 759.73299 -1088.3409 0.99117155 -0.34780329 0.512
7600 -1853.6532 764.84642 -1088.8067 0.99784269 -0.098590718 0.512
7700 -1876.6886 756.38707 -1120.3016 0.98680636 -0.17912577 0.512
7800 -1857.6403 719.20424 -1138.4361 0.93829647 -0.32247855 0.512
7900 -1891.2369 707.44358 -1183.7933 0.92295314 -0.44928961 0.512
8000 -1930.5545 747.85472 -1182.6997 0.97567478 -0.2607688 0.512
8100 -1931.3403 744.07929 -1187.261 0.97074924 -0.36763161 0.512
8200 -1920.9036 757.0399 -1163.8637 0.98765806 -0.29103201 0.512
8300 -1904.5561 747.57535 -1156.9807 0.9753103 -0.38464012 0.512
8400 -1844.7405 820.31281 -1024.4277 1.0702059 -0.044405706 0.512
8500 -1860.3078 809.13555 -1051.1723 1.0556237 -0.018849627 0.512
8600 -1841.1531 776.85955 -1064.2935 1.0135154 -0.080192818 0.512
8700 -1860.6583 785.807 -1074.8513 1.0251885 -0.29734141 0.512
8800 -1841.0455 779.78036 -1061.2651 1.017326 -0.11420405 0.512
8900 -1887.3837 878.92659 -1008.4571 1.1466753 -0.34666733 0.512
9000 -1879.4834 767.25891 -1112.2245 1.0009901 -0.3331713 0.512
9100 -1900.1999 818.54475 -1081.6552 1.0678992 -0.19458572 0.512
9200 -1882.1203 794.90843 -1087.2118 1.0370625 -0.25879106 0.512
9300 -1893.5664 783.13068 -1110.4357 1.0216969 -0.25735285 0.512
9400 -1893.5147 756.00962 -1137.5051 0.98631392 -0.26461519 0.512
9500 -1908.8115 742.60538 -1166.2061 0.96882633 -0.4468834 0.512
9600 -1887.0565 762.24949 -1124.807 0.99445465 -0.36695082 0.512
9700 -1878.5858 771.53563 -1107.0502 1.0065696 -0.2300855 0.512
9800 -1848.4047 752.27373 -1096.1309 0.98143997 -0.28729274 0.512
9900 -1865.561 731.41466 -1134.1464 0.95422656 -0.3874617 0.512
10000 -1887.2808 787.80237 -1099.4784 1.0277917 -0.26779032 0.512
Loop time of 1.67987 on 1 procs for 8000 steps with 512 atoms
Performance: 2057303.356 tau/day, 4762.276 timesteps/s
98.6% CPU use with 1 MPI tasks x no OpenMP threads
MPI task timing breakdown:
Section | min time | avg time | max time |%varavg| %total
---------------------------------------------------------------
Pair | 1.1024 | 1.1024 | 1.1024 | 0.0 | 65.62
Bond | 0.00062656 | 0.00062656 | 0.00062656 | 0.0 | 0.04
Neigh | 0.40537 | 0.40537 | 0.40537 | 0.0 | 24.13
Comm | 0.067369 | 0.067369 | 0.067369 | 0.0 | 4.01
Output | 0.040565 | 0.040565 | 0.040565 | 0.0 | 2.41
Modify | 0.051896 | 0.051896 | 0.051896 | 0.0 | 3.09
Other | | 0.01168 | | | 0.70
Nlocal: 512 ave 512 max 512 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Nghost: 1398 ave 1398 max 1398 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Neighs: 12036 ave 12036 max 12036 min
Histogram: 1 0 0 0 0 0 0 0 0 0
Total # of neighbors = 12036
Ave neighs/atom = 23.5078
Ave special neighs/atom = 0
Neighbor list builds = 800
Dangerous builds = 800
Total wall time: 0:00:02
[3]:
%matplotlib inline
import freud
from matplotlib import pyplot as plt
import numpy as np
import warnings
[4]:
with warnings.catch_warnings():
warnings.simplefilter('ignore')
# We read the number of particles, the system box, and the
# particle positions into 3 separate arrays.
N = int(np.genfromtxt(
'output_custom.xyz', skip_header=3, max_rows=1))
box_data = np.genfromtxt(
'output_custom.xyz', skip_header=5, max_rows=3)
data = np.genfromtxt(
'output_custom.xyz', skip_header=9,
invalid_raise=False)
# Remove the unwanted text rows
data = data[~np.isnan(data).all(axis=1)].reshape(-1, N, 6)
box = freud.box.Box.from_box(
box_data[:, 1] - box_data[:, 0])
# We shift the system by half the box lengths to match the
# freud coordinate system, which is centered at the origin.
# Since all methods support periodicity, this shift is simply
# for consistency but does not affect any analyses.
data[..., :3] -= box.L/2
rdf = freud.density.RDF(rmax=4, dr=0.03, rmin=1)
for frame in data:
rdf.accumulate(box, frame[:, :3])
msd = freud.msd.MSD(box)
msd.compute(positions=data[:, :, :3], images=data[:, :, 3:])
# Plot the RDF
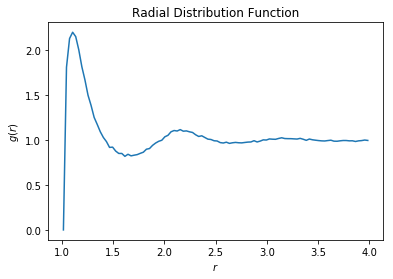
plt.plot(rdf.R, rdf.RDF)
plt.title('Radial Distribution Function')
plt.xlabel('$r$')
plt.ylabel('$g(r)$')
plt.show()
# Plot the MSD
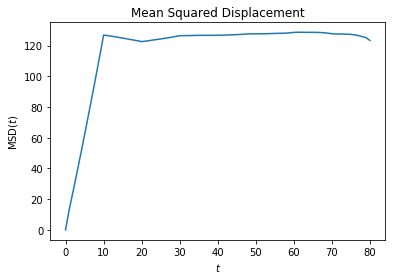
plt.plot(msd.msd)
plt.title('Mean Squared Displacement')
plt.xlabel('$t$')
plt.ylabel('MSD$(t)$')
plt.show()